Formula For Volume Of A Rectangular Prism With Fractions

Beginning geometry students commonly have to find the volume and the surface area of a cube and a rectangular prism. To accomplish the task, the student has to memorize and understand the application of formulas that apply to these three-dimensional figures. Volume refers to the amount of space inside the object, measured in cubic units, while surface area measures the total amount in square units of each object's six faces. It is also important to state your answer using the proper units, since not doing so will typically result in the question being marked partially or completely wrong. Gem is reading the latest issue of Better Caves and Firepits magazine. Stone blocks used to be popular decoration, but the world has moved on!

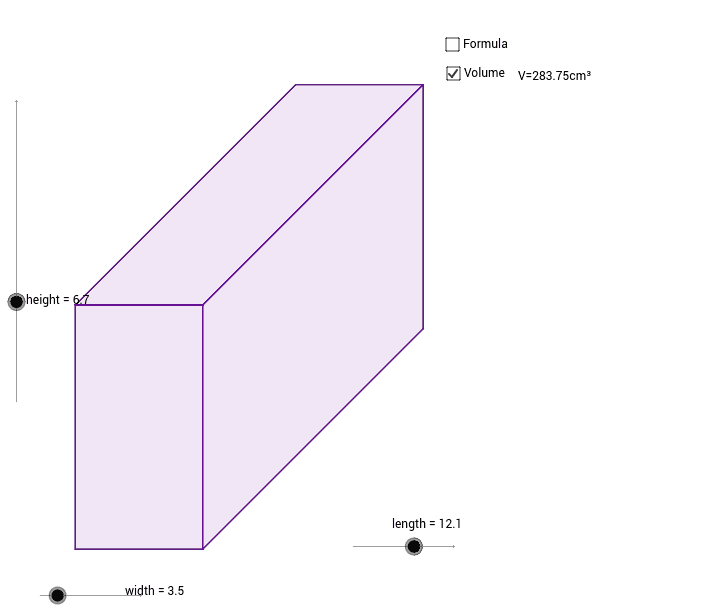
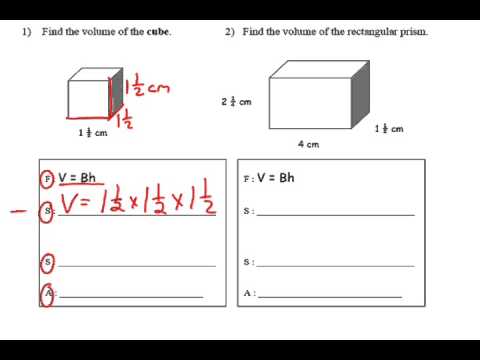
Unless they want to be cultural dinosaurs, Gem's husband Rocky must remove his stone collection. Rocky is attached to his stones but he has an idea! He can try to fit all his stones in his storage cave. If Rocky can calculate the volume of a rectangular prism using the area of the base he just might fit all his stone blocks in storage. The formula for the volume of a rectangular prism is length times width times height. The volume of the first block is the length, 5 times the width, 2 times the height which is also 2.

Notice that each prism has the same length and width. In each case, we first multiplied 5 times 2 to get 10. This leads to another way of thinking about the volume of a rectangular prism. The base of each prism is the face on the bottom.

And so the height is the side length perpendicular to the base. To find the total volume, we multiply 10 times the height of each prism. In general, we can calculate the volume of a prism by finding the area of the base times the height. We can use this equation anytime we are calculating the volume of a prism. Rocky tries to neatly fit his beloved blocks into his storage cave.

But some of the blocks will need to be flipped on their sides so they can fit properly. Rocky is a bit concerned--will the volumes still be the same if a different face is on the bottom? With the 5 by 2 face as the base the area of the base is 10 the volume is the base times the height, 7 giving us a volume of 70 cubic inches. It's the new base of the prism, and the area of the base is 7 times 2 or 14 square inches.

Multiplying 14 times the new height of 5 gives us a volume of 70 cubic inches, as before. Let's flip the block one more time so that the 7 by five face is the base. The area of the base is 7 times 5 or 35 square inches. Multiplying 35 times the new height of 2 confirms the volume of 70 cubic inches.

With a rectangular prism, any face can be the base and the volume can be computed by calculating the area of the base times the height. Rocky can flip his blocks freely without changing the volume--that makes his work easier! Let's review our tools for calculating the volume of a rectangular prism. We can calculate the volume as length times width times height. We can also select any face of a rectangular prism as the base.

We then calculate the area of the base, and multiply by the height. Rocky has efficiently stored all his stones, and Gem is very grateful. She tells him that he can keep his stones in storage there for as long as he likes. Mmm if only they knew it was just an ordinary caveman cleaning his cave. In this lesson students will extend their knowledge of volume from using whole numbers to using fractional units. Find volume of rectangular prisms with whole number and fractional edge lengths using unit and fractional unit cubes.

This two-day lesson uses a hands-on problem solving approach to find the volume of a right rectangular prism with fractional edges. Students first design boxes and fill with Rubik's Cubes. They create a formula from the patterns they found. Using cubes with fractional edges requires students to apply fractional units to their formula.

To find the volume of the rectangular prism, we multiply the length by the breadth. To find the area of the two dimensional figure at the base and then measure the 3D solid by multiplying again by the height. Length times width times height would give you the volume of any rectangular prism. And once you enter the third dimension your measurements have to be in cubic units like these cubic centimeters. I show how we can indeed calculate the VOLUME of right rectangular prisms with fractional edge lengths by multiplying the three dimensions length, width, and height.

Students need multiple opportunities to measure volume by filling rectangular prisms with blocks and looking at the relationship between the total volume and the area of the base. Through these experiences, students review the volume formula . Students can explore the connection between filling a box with unit cubes and the volume formula using interactive applets such as the Cubes Toolon NCTM's Illuminations (5.MD.C.5) . Use this sixth-grade geometry worksheet to give students plenty of practice finding the volume of rectangular prisms using the volume formula. Mentally decompose and recompose a right rectangular prism built from cubes into layers, each of which is composed of rows and columns. The height of the prism determines how many layers would fit in the prism.

The formula for volume can be derived as length times width times height, or the area of the base times the height. In this lesson, we find the volume of rectangular prisms with fractional edge lengths. Mathematical problems involving rectangular prisms with fractional edge lengths. Calculating the volume of rectangular prisms is a new skill that is introduced in 5th grade. Students will apply mathematical formulas to find the volume of different kinds of figures and also determine the volume of a figure composed of two connected rectangular prisms.

Learners will also work with other kinds of measurement when they make larger or smaller versions of figures and learn to convert measurements. This lesson uses a discovery approach to exploring the meaning of volume. The students will utilize math practice standards and cubes as they construct and analyze the relationship between the length, width, and height to the total amount of cubes.

Prisms in items must be right rectangular prisms. Unit fractional edge lengths for the unit cubes used for packing must have a numerator of 1. Follow Cindy as she explores fractional unit cubes and finds the volume of rectangular prisms that have rational number dimensions in this interactive tutorial. To rectangular prisms with whole number side lengths. In this lesson, students recall these formulas, demonstrate their equivalence, and extend their work to include rectangular prisms with fractional side lengths.

It's 1 over the least common multiple of the denominators. This tells us that each of our unit cubes has a teeny tiny volume of ft3. A unit of volume, a cube with a side length of 1 unit, is called a unit cube. Side lengths can be fractions and mixed numbers. Recognize volume as an attribute of a solid figure. Use unit cubes as a basis for students' understanding of volume as a measurable attribute.

Volume is comprised of layers of measurable units. Use standard units of measurement cubic cm, cubic in, cubic ft, and any unit that the problem presents. In this lesson, students extend this idea to prisms with fractional side lengths. The volume is the number of unit-fraction cubes in the prism times the volume of each unit-fraction cube. Students show that this result is the same as the volume found by using the formula. This lesson introduces the idea of finding volume.

Students will be left to design their own data collection and organizing the data that they collect. They will apply the skill of finding volume to using fractional parts of a number and finding the product using the volume formula. We can now fill up our rectangular prism these unit cubes. The volume of rectangular prism, then, is ft3, or ft3.

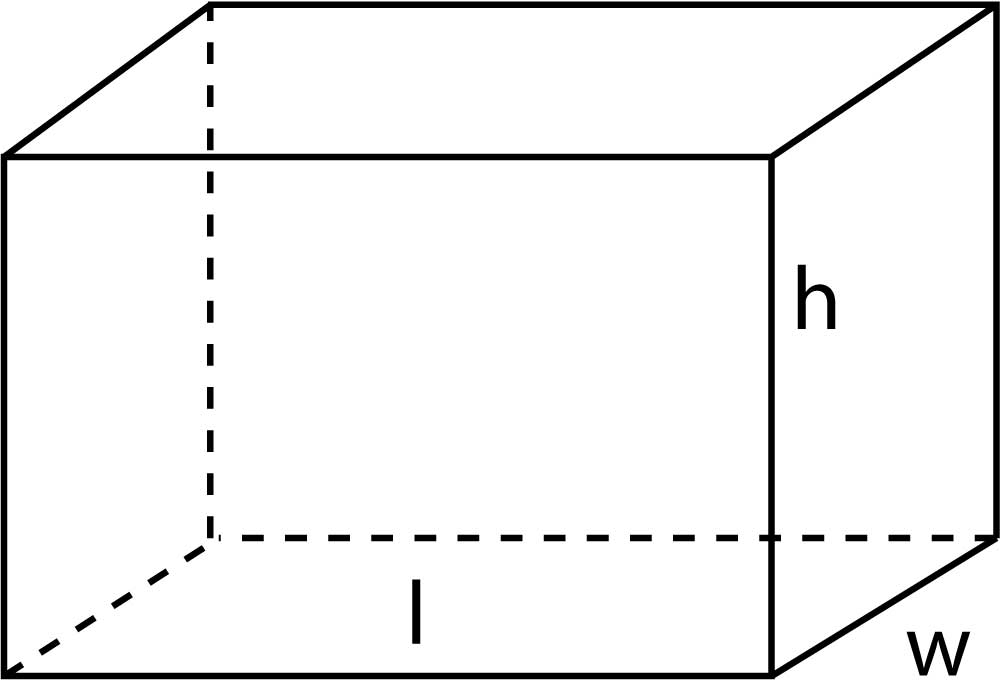
Lo and behold, if we multiply our length, width, and height together, we'll get the same answer. Use this sixth-grade geometry worksheet to help students cement their understanding of how to find the volume of a rectangular prism with fractional side lengths. A prism is a three dimensional figure with two faces that are congruent and sides that are parallelograms. A prism is named after the shape of the two identical faces or bases. Arectangular prismhas two faces in the shape of a rectangle.

Some common examples of rectangular prisms in real life are, cereal boxes, Kleenex boxes, shipping containers, dice, and aquariums. With this volume of a rectangular prism calculator - a.k.a. a box volume calculator - you'll find the volume of any box-shaped container in a blink of an eye. You need to enter only three values, and we'll calculate the volume for you (though it's not so tricky, you could figure it yourself😊). If you're searching for the definition, check the section What is a rectangular prism.

The volume of a rectangular prism is the measurement of the total space inside it. Imagine a rectangular container filled with water. In this case, the total quantity of water that the container can hold is its volume. A prism is a polyhedron having identical bases, flat rectangular side faces, and the same cross-section all along its length.

Prisms are classified as per the shape of their base. A rectangular prism is categorized as a three-dimensional shape. It has six faces and all the faces of the prism are rectangles.

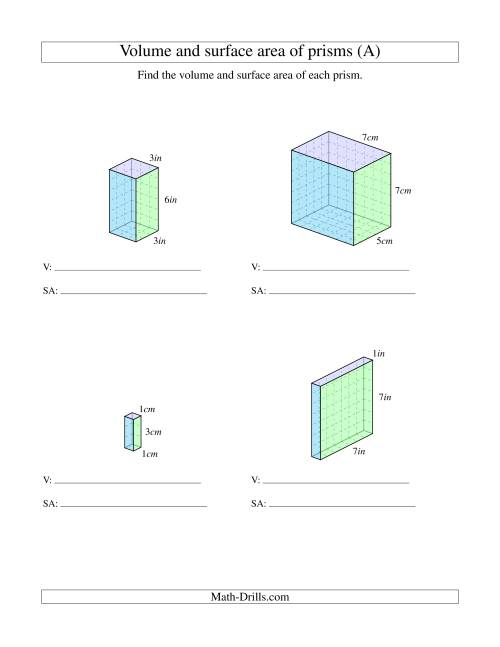
Let us learn the formula to find the volume of a rectangular prism in this article. Volume is the amount of 3-dimensional space an object occupies. To find the volume of a rectangular prism, we multiply the length of the prism by the width of the prism by the height of the prism. Determine the formulas for finding volume of rectangular prisms and use the formulas to solve for volume. Apply the formula for volume of right rectangular prism or cube to find volume of solids. Multiply length times width times height to find the volumes of the 30 rectangular prisms on these task cards.

Advanced level includes one or more decimal measurements on each shape. As always, we also want students to be able to apply this understanding to real-world situations. So long as students working with rectangular prisms with non-whole-number dimensions, they're good to go.

Assuming, of course, that they're using the right units and interpreting their answers properly. That formulas exist to assist us in finding the volume of rectangular prisms. Help your students visualize rectangular prisms with this exercise. Students will practice modeling rectangular prisms and calculating the volume of each shape using the formula.

Before calculating the volume of a rectangular prism using the formula, we need to make sure that all the dimensions are of the same units. The following steps are used to calculate the volume of a rectangular prism. The formulas for volumes of various kinds of square-based pyramids can be modified to give formulas for pyramids formed by cutting off a corner of a cube.

The dimension of the space again appears in the denominator of the formula, but in a new way. Cutting off one corner of a square produces a triangle with half the area. Cutting off one corner of a cube produces a pyramid with a triangular base.

We can obtain this same triangular pyramid by decomposing a square-based pyramid into four pieces. If we approximate the square-based pyramid by a stack of square slabs, then the triangular pyramid is approximated by a stack of triangular slabs each with half the volume. In general then-dimensional volume of a corner figure of an n-cube will be 1/n! Stands for "n factorial," obtained by, multiplying together the first n numbers.

The analogy between the decomposition of the square in the plane and the cube in space gave us a way to find the volume formula for an off-center pyramid with a square base. A square is divided into two congruent triangles by a diagonal, and so is a rectangular region. Learners will find the volume of different rectangular prisms by counting up how many cubic units were used to make each figure.

A flat shaped like, a rectangle has two dimensions, length and width. The height is what we were measuring when we counted the layers upwards and again because we built the shape from centimeter cubes. We know that each cube side measures one centimeter. Find volume or any of the edges by manipulating the formula for volume to find one other.

Find the total volume of solid figures composed of two right rectangular prisms. In this explainer, we will learn how to calculate volumes of rectangular prisms and cubes given their dimensions and solve problems including real-life situations. Students are asked to determine the volume of a right rectangular prism given fractional edge lengths.